Stellar Line Formation

By Steven R. Cranmer (Harvard University). May, 2013.
Edit by Yuan-Sen Ting (Harvard University).

---

         A simple, but instructive, way to think about the formation of spectral lines is the Schuster (1905) reversing layer model (see also Mihalas 1978, 1999). The spectral line (i.e., a particular transition from one bound electron energy level in an element to another energy level) is assumed to be formed in a "cloud" of gas sitting "above" the main source of radiation. That main part -- which has traditionally been thought of as a dense stellar photosphere, but can be any other background radiation source -- is assumed to produce a broad spectral continuum. We also assume that the properties of the line-absorbing (or line-emitting) gas are constant throughout the cloud. If the thickness of the cloud is given by \(\Delta z\), then the dimensionless optical depth in the cloud can be written \begin{equation} \tau_\nu = \kappa_\nu \rho \Delta z = \kappa_{\mathrm{\small L}} \phi (\nu) \rho \Delta z , \end{equation} where \(\nu\) is the photon frequency, \(\kappa_\nu\) is the absorption coefficient in units of cross section per unit mass (e.g., cm\(^2\) g\(^{-1}\)), and \(\rho\) is the mass density. For convenience, we write the absorption coefficient as \(\kappa_\mathrm{\small L} \phi (\nu)\), which separates the total line opacity \(\kappa_\mathrm{\small L}\) from the line broadening coefficient \(\phi(\nu)\).

         The solution for the specific intensity \(I_\nu\) that emerges from the Schuster cloud is given by \begin{equation} I_\nu = I_{0\nu} e^{-\tau_\nu} + S_\nu ( 1- e^{-\tau_\nu}) , \end{equation} where \(I_{0\nu}\) is the intensity of the continuum that enters the cloud from below and \(S_\nu\) is the so-called source function of the cloud; it takes account of the local properties of the cloud that would make it "glows" on its own, even in the absence of an external source of radiation. We can continue to make simplifying approximations about these two intensity parameters, and in many cases it is useful to think about them as blackbody Planck spectra. Thus, let us use the shorthand \begin{equation} I_{0 \nu} \simeq B_{\mathrm{\small C}} ( T_{\mathrm{\small C}} ), \qquad S_\nu \simeq B_{\mathrm{\small L}} ( T_{\mathrm{\small L}}), \end{equation} where the subscript "C" denotes the conditions in the background medium where the continuum is formed, and "L" denotes the conditions in the Schuster cloud where the line is formed. In local thermodynamic equilibrium, \(B\propto T^4\), so we can rewrite equation (2) in terms of the dimensionless residual intensity \(r_\nu\) as \begin{equation} r_\nu = \frac{I_\nu}{I_{0\nu}} = e^{-\tau_\nu} + \bigg(\frac{T_{\mathrm{\small L}}}{T_\mathrm{\small C}}\bigg)^4 (1- e^{-\tau_\nu}). \end{equation} One can see that if the temperature in the cloud is lower than the temperature in the underlying continuum photosphere (i.e., \(T_{\mathrm{\small L}}/T_{\mathrm{\small C}} < 1\)) that \(r_\nu <1\) and we will have an absorption line. Conversely, if the cloud is hotter than the underlying continuum region, we will have an emission line with \(r_\nu >1\).

         We characterize a line's total amount of absorption or emission by integrating over frequency. Thus, we define the equivalent width \begin{equation} W_\nu = \int \mathrm{d}\nu \; (1- r_\nu). \end{equation} Note that in this case the subscript \(\nu\) does not mean that \(W_\nu\) is a function of \(\nu\), but it is there to convey that this quantity has units of frequency. For the standard case of a cold cloud that produces an absorption line, we see that as the number of atoms (hence the column density) in the line-forming cloud increases, the line gets deeper, and the (positive definite) equivalent width grows in magnitude. The dependence of \(W_\nu\) on the total line opacity is known as the curve of growth.

---

Line broadening processes

         The shape of the curve of growth depends crucially on the line broadening function \(\phi(\nu)\). The simplest possible picture of atomic transitions assumes that the two energy levels have precisely known energies \(E_1\) and \(E_2\). Thus, the transition occurs only when photons of a single frequency \(\nu_{\small 12}\) are involved, with \begin{equation} E_2 - E_1 = h \nu_{\small 12} \end{equation} where \(h\) is the Planck's constant. In a cloud of gas with a finite temperature, the individual atoms are all moving around with random velocities in 3D space. In kinetic theory we describe the microscopic motions of the atoms with a distribution function \(f\) written as a function of the particle vector momentum \(\mathbf{p}\). In most "well-behaved" systems this function is a Maxwell-Boltzmann distribution, \begin{equation} f(\mathbf{p}) = \frac{n}{(2\pi mkT)^{3/2}} \exp \bigg( - \frac{p^2}{2 m kT} \bigg) \end{equation} where \(m\) is the particle mass, \(n=\rho/m\) is the number density, \(k\) is the Boltzmann's constant, and \(T\) is the temperature.

         The line profile function for pure Doppler broadening is \begin{equation} \langle \phi (\nu_{\mathrm{\small obs}}) \rangle = \frac{1}{\Delta \nu_{\mathrm{\small D}}\sqrt{\pi}} e^{-x^2} \end{equation} where we define the dimensionless line frequency \(x\) and the Doppler width \(\Delta \nu_{\mathrm{\small D}}\) as \begin{equation} x = \frac{\nu_{\mathrm{\small obs}}- \nu_{\mathrm{\small 12}}}{\Delta \nu_{\mathrm{\small D}}}, \qquad \Delta v_{\mathrm{\small D}} = \frac{\nu_{\small 12}}{c} \sqrt{\frac{2kT}{m}}. \end{equation}

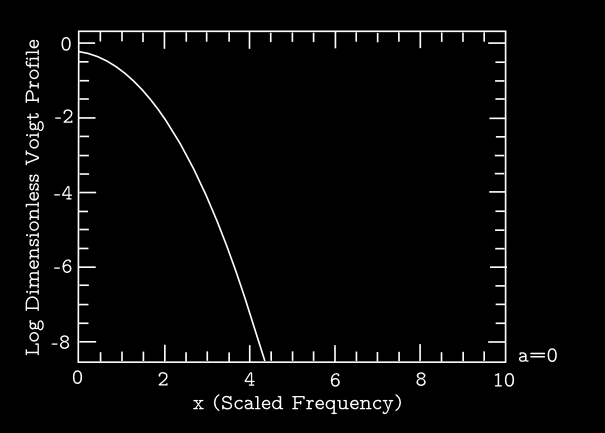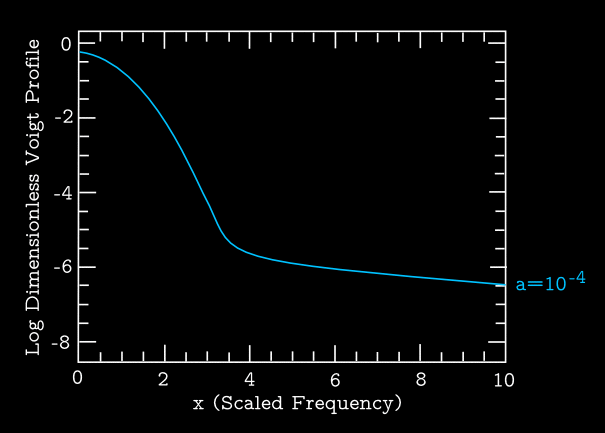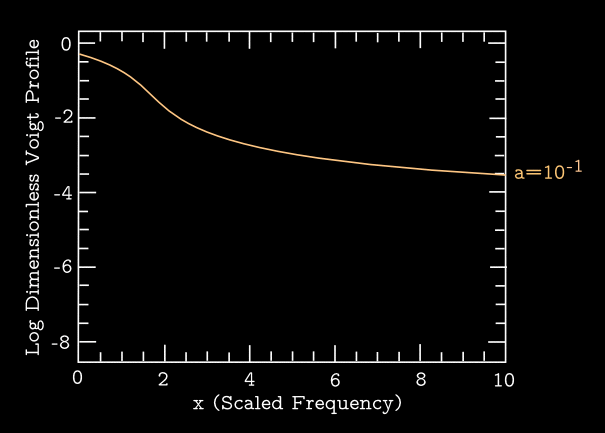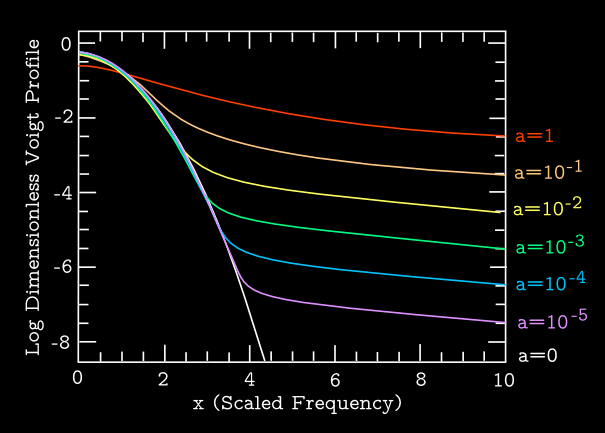
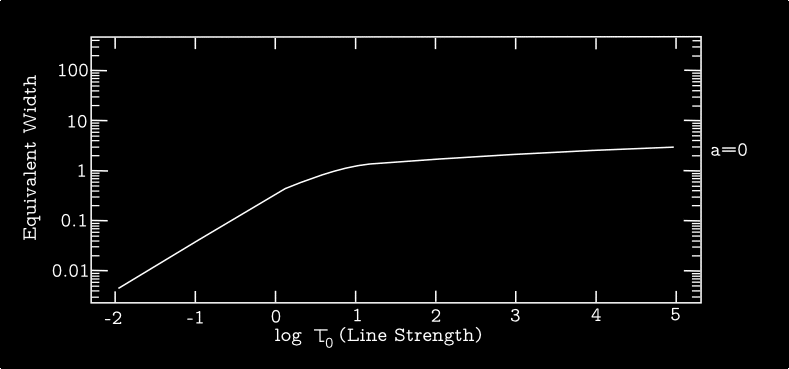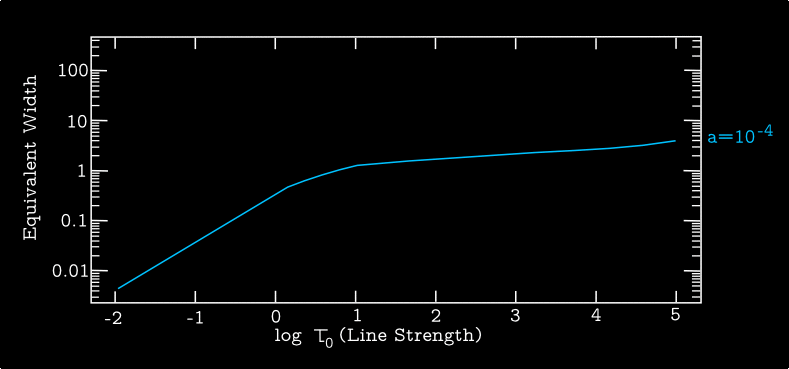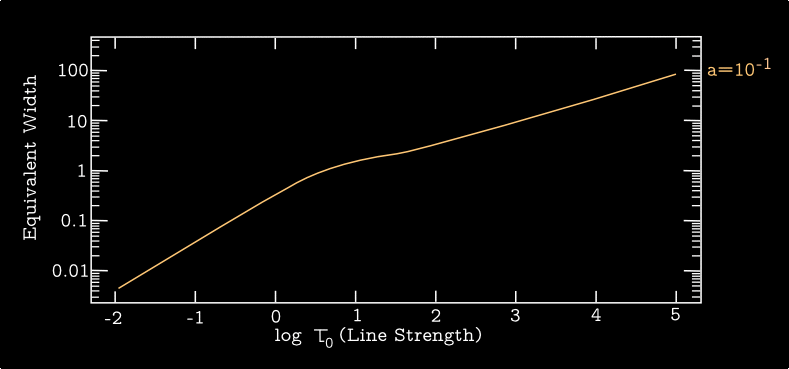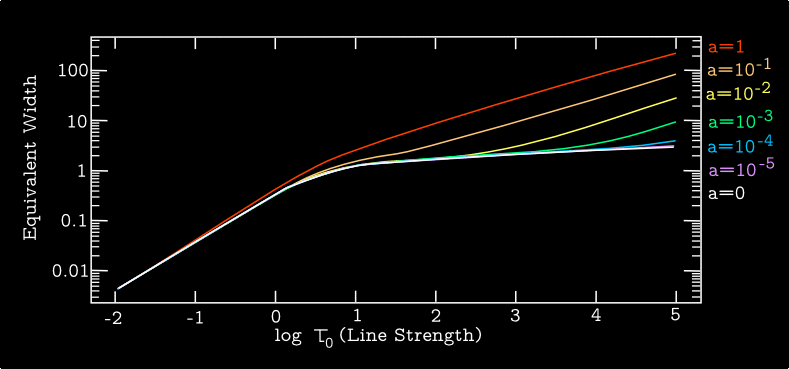
         When combined with natural broadening, the profile becomes a Voigt function: \begin{equation} \langle \phi (\nu_{\mathrm{\small obs}}) \rangle = \frac{\widetilde{H}(a,x)}{\Delta \nu_{\mathrm{\small D}}} \end{equation} and the normalized version of the Voigt function is defined as \begin{equation} \widetilde{H}(a,x) = \frac{a}{\pi^{3/2}}\int^{+\infty}_{-\infty} \frac{\mathrm{d}y \, e^{-y^2}}{(x-y)^2 + a^2} \end{equation} where the dimensionless "damping constant" \(a= \gamma/(4\pi \Delta \nu_{\mathrm{\small D}})\) is a ratio that conveys the relative importance of the two sources of line broadening.

---

Evaluating the curve of growth

         The curve of growth shows weak lines exhibiting \(W_\nu \propto \tau_0\) (the linear part), saturated lines showing \(W_\nu \propto \sqrt{\ln \tau_0}\) (the flat part), and strong lines with Voigt wings showing \(W_\nu \propto \sqrt{\tau_0}\).

---

References

---